Backward Function - Entire Graph
from graphviz import Digraph
def trace(root):
#Builds a set of all nodes and edges in a graph
nodes, edges = set(), set()
def build(v):
if v not in nodes:
nodes.add(v)
for child in v._prev:
edges.add((child, v))
build(child)
build(root)
return nodes, edges
def draw_dot(root):
dot = Digraph(format='svg', graph_attr={'rankdir': 'LR'}) #LR == Left to Right
nodes, edges = trace(root)
for n in nodes:
uid = str(id(n))
#For any value in the graph, create a rectangular ('record') node for it
dot.node(name = uid, label = "{ %s | data %.4f | grad %.4f }" % ( n.label, n.data, n.grad), shape='record')
if n._op:
#If this value is a result of some operation, then create an op node for it
dot.node(name = uid + n._op, label=n._op)
#and connect this node to it
dot.edge(uid + n._op, uid)
for n1, n2 in edges:
#Connect n1 to the node of n2
dot.edge(str(id(n1)), str(id(n2)) + n2._op)
return dot
import math
class Value:
def __init__(self, data, _children=(), _op='', label=''):
self.data = data
self.grad = 0.0
self._backward = lambda: None #Its an empty function by default. This is what will do that gradient calculation at each of the operations.
self._prev = set(_children)
self._op = _op
self.label = label
def __repr__(self): # This basically allows us to print nicer looking expressions for the final output
return f"Value(data={self.data})"
def __add__(self, other):
out = Value(self.data + other.data, (self, other), '+')
def backward():
self.grad = 1.0 * out.grad #Remember we are doing chain rule here, hence the product with out.grad
other.grad = 1.0 * out.grad
out._backward = backward
return out
def __mul__(self, other):
out = Value(self.data * other.data, (self, other), '*')
def backward():
self.grad = other.data * out.grad #Remember we are doing chain rule here, hence the product with out.grad
other.grad = self.data * out.grad
out._backward = backward
return out
def tanh(self):
x = self.data
t = (math.exp(2*x) - 1)/(math.exp(2*x) + 1)
out = Value(t, (self, ), 'tanh')
def backward():
self.grad = 1 - (t**2) * out.grad #Remember we are doing chain rule here, hence the product with out.grad
out._backward = backward
return out
#Inputs x1, x2 of the neuron
x1 = Value(2.0, label='x1')
x2 = Value(0.0, label='x2')
#Weights w1, w2 of the neuron - The synaptic values
w1 = Value(-3.0, label='w1')
w2 = Value(1.0, label='w2')
#The bias of the neuron
b = Value(6.8813735870195432, label='b')
x1w1 = x1*w1; x1w1.label = 'x1*w1'
x2w2 = x2*w2; x2w2.label = 'x2*w2'
#The summation
x1w1x2w2 = x1w1 + x2w2; x1w1x2w2.label = 'x1*w1 + x2*w2'
#n is basically the cell body, but without the activation function
n = x1w1x2w2 + b; n.label = 'n'
#Now we pass n to the activation function
o = n.tanh(); o.label = 'o'
o.grad = 1.0 #This is the base case, we set this
draw_dot(o)
Instead of calling the '_ backward' function each time, we are creating it as a function in the Value object itself.
Now, we also need to make sure that all the nodes have been accessed and forward pass through. So, we have used a concept called 'topological sort' where all the nodes are accessed/traversed in the same/one direction (either left-to-right or vice-versa)
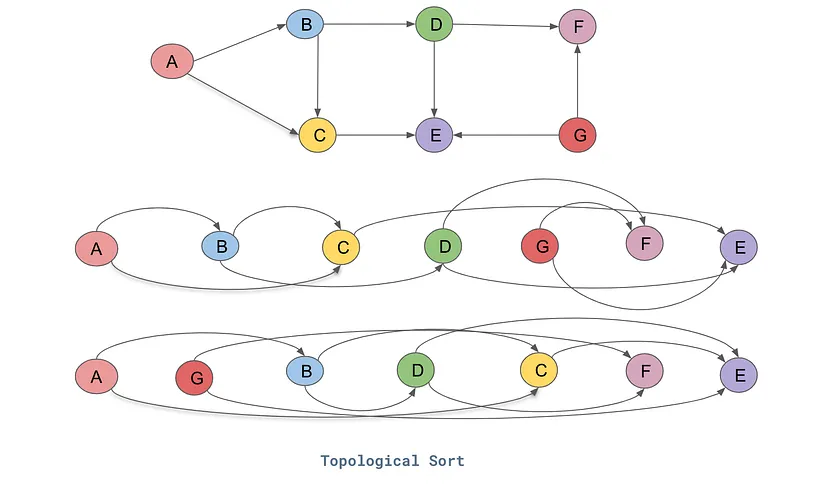
Therefore, we are adding the code for it, where it ensures that all the nodes are accessed at least once (and only stored once) and the node is only stored after/when all of it's child nodes are accessed and stored. This way we know we have traversed through the entire graph.
topo = []
visited = set() #We are maintaining a set of visited nodes
def build_topo(v):
if v not in visited:
visited.add(v)
for child in v._prev:
build_topo(child)
topo.append(v) #Adds itself, only after all its children have been added
build_topo(o) #We are starting from the root node, for us 'o'
topo
[Value(data=6.881373587019543), Value(data=1.0), Value(data=0.0), Value(data=0.0), Value(data=-3.0), Value(data=2.0), Value(data=-6.0), Value(data=-6.0), Value(data=0.8813735870195432), Value(data=0.7071067811865476)]
Once all the nodes have been topologically sorted, we then reverse the nodes order (Since we are traversing it from left to right i.e. input to output, we are reversing it, so that the gradients are calculated. As we have done previously in our examples) call the '_ backward' function to perform backpropagation from the output.
for node in reversed(topo):
node._backward()
And now, we will add all the calculated gradients to the graph!
draw_dot(o)
Now, we add this functionality to our value object
import math
class Value:
def __init__(self, data, _children=(), _op='', label=''):
self.data = data
self.grad = 0.0
self._backward = lambda: None #Its an empty function by default. This is what will do that gradient calculation at each of the operations.
self._prev = set(_children)
self._op = _op
self.label = label
def __repr__(self):
return f"Value(data={self.data})"
def __add__(self, other):
out = Value(self.data + other.data, (self, other), '+')
def backward():
self.grad = 1.0 * out.grad
other.grad = 1.0 * out.grad
out._backward = backward
return out
def __mul__(self, other):
out = Value(self.data * other.data, (self, other), '*')
def backward():
self.grad = other.data * out.grad
other.grad = self.data * out.grad
out._backward = backward
return out
def tanh(self):
x = self.data
t = (math.exp(2*x) - 1)/(math.exp(2*x) + 1)
out = Value(t, (self, ), 'tanh')
def backward():
self.grad = 1 - (t**2) * out.grad
out._backward = backward
return out
def backward(self):
topo = []
visited = set()
def build_topo(v):
if v not in visited:
visited.add(v)
for child in v._prev:
build_topo(child)
topo.append(v)
build_topo(self)
self.grad = 1.0
for node in reversed(topo):
node._backward()
This is the updated value object^
Cross-verifying it once
#I re-run the cells containing the node values as well
draw_dot(o)
o.backward()
draw_dot(o)